

Simplifying Radicals A Radical Expression is Simplified When the Following Are All True No perfect powers are factors of the radicand and all exponents in the radicand are less than the index. Simplifying Radicals Simplify by rationalizing the denominator: The conjugate of a binomial is a binomial having the same two terms with the sign of the second term changed. This is done by using the conjugate of the denominator. Cannot be simplified further.Ĭonjugates When the denominator of a rational expression is a binomial that contains a radical, the denominator is rationalized. Rationalizing Denominators Examples : To Rationalize a Denominator Multiply both the numerator and the denominator of the fraction by a radical that will result in the radicand in the denominator becoming a perfect power. Notice that the inner and outer terms cancel. Multiplying Radicals Multiply: Use the FOIL method. To Add or Subtract RadicalsĬAUTION! The product rule does not apply to addition or subtraction! Combine like radicals (if there are any).
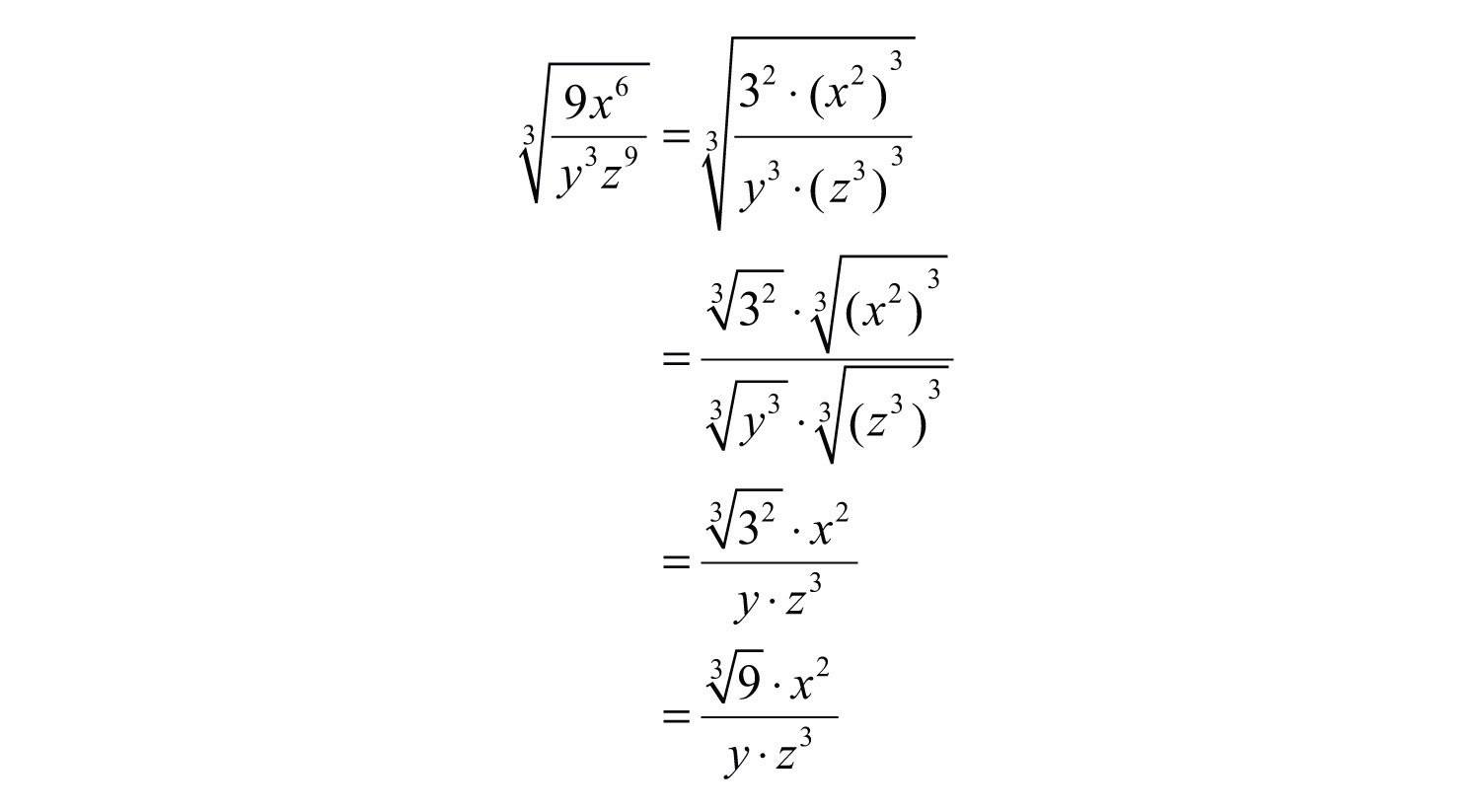
Example: Cannot be simplified further.Īdding & Subtracting Examples: Simplify each radical expression. They are added the same way like terms are added. Like Radicals Like radicals are radicals having the same radicands. Quotient Rule for Radicals More Examples:Īdding, Subtracting, and Multiplying Radicals Quotient Rule for Radicals Examples: Simplify radicand, if possible. Product Rule for Radicals Examples: *When the radical is simplified, the radicand does not have a variable with an exponent greater than or equal to the index. To Simplify Radicals Using the Product Rule Simplify the radical containing the perfect powers. Place all the perfect powers under the same radical. Use the product rule to write the radical expression as a product of radicals. Write each variable factor as a product of two factors, one of which is the largest perfect power of the variable for the index. Product Rule for Radicals If the radicand contains a coefficient other than 1, write it as a product of the two numbers, one of which is the largest perfect power for the index. The radicand x n is a perfect power when n is a multiple of the index of the radicand. This idea can be expanded to perfect powers of a variable for any radicand. Example : Since the exponent, 20, is divisible by the index, 5, x 20 is a perfect fifth power. Perfect Powers A quick way to determine if a radicand x n is a perfect power for an index is to determine if the exponent n is divisible by the index of the radical. 1, 8, 27, 64, 125, and 216 are the first six perfect cubes. A perfect cube is the cube of a natural number. 1, 4, 9, 16, 25, and 36 are the first six perfect squares. Multiply by the \(\sqrt-1\) Exercises for Simplifying Radical Expressions Involving Fractions Simplify radical expressions.Simplifying radical expressions, rational exponents, radical equationsĭefinitions A perfect square is the square of a natural number. Simplifying Radical Expressions Involving Fractions – Example 1: If there is a radical and another integer in the denominator, multiply both numerator and denominator by the conjugate of the denominator.If there is a radical in the denominator, multiply the numerator and denominator by the radical in the denominator.To simplify radical expressions involving fractions: Step by Step Guide to Simplifying Radical Expressions Involving Fraction To rationalize the denominator, you need to get rid of all radicals that are in the denominator. + Ratio, Proportion and Percentages PuzzlesĪ radical contains an expression that is not a perfect root it is called an irrational number.


 0 kommentar(er)
0 kommentar(er)
